Menentukan Nilai Optimum Dengan Garis Selidik. Tentukan garis selidik ax + by = k apabila. Suatu titik dalam poligon dimana f mencapai nilai maksimum atau minimum dinamakan penyelesaian optimum. Metode garis selidik adalah sebuah metode yang umum digunakan dalam program linear untuk menentukan nilai optimum dari suatu persoalan linear. Selain metode uji titik pojok, cara lain yang dapat digunakan untuk mengetahui nilai optimum adalah metode garis selidik.
Menentukan nilai optimum dengan Garis selidik YouTube From youtube.com
Tentukan garis selidik ax + by = k apabila. Tentukan garis selidik ax + by = k apabila. Intinya, cara yang dapat dilakukan untuk mencari nilai optimum dengan garis selidik yang diperoleh dari persamaan fungsi objektif atau fungsi tujuannya. Nilai optimum akan mencapai salah satu titik ekstrim (titik sudut) di tempat garis selidik itu menyinggung. Menentukan nilai optimum program linier dengan metode garis selidik. Tentukan model pertidaksamaan dari informasi soal dan gambarkan daerah selesaian dari sistem pertidaksamaan tersebut pada bidang koordinat.
Dengan mengalikan kedua ruas persamaan garis selidik dengan 10.000, kamu mendapatkan nilai maksimum fungsi objektif.
Cara menentukan nilai optimum dapat menggunakan metode: Metode uji titik pojok dan b. Jika garis selidik yang melalui titik singgung berada paling jauh dari titik o(0,0), maka fungsi tujuan yang dicapai ialah nilai maksimum. Nilai z diberikan sembarang nilai. Jika bentuk umum fungsi tujuan dinotasikan dengan z = f ( x, y) = a x + b y maka bentuk umum garis selidik dinotasikan dengan a x + b y = k, dengan k ∈ r dimana k sembarang bilangan yang kita pilih. Tentukan garis selidik ax + by = k apabila.
Source: python-belajar.github.io
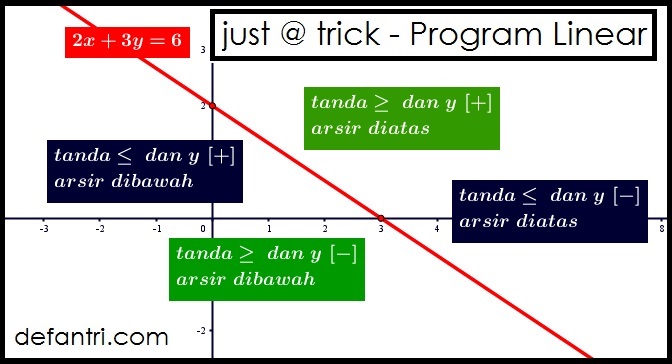
Dengan mengalikan kedua ruas persamaan garis selidik dengan 10.000, kamu mendapatkan nilai maksimum fungsi objektif. Dengan mengalikan kedua ruas persamaan garis selidik dengan 10.000, kamu mendapatkan nilai maksimum fungsi objektif. Untuk titik (120,30) diperoleh z = 270 maka persamaan garis selidik pertama adalah. Menentukan nilai optimum program linier dengan metode garis selidik. Perhatikan bahwa garis selidik yang menyebabkan fungsi objektif maksimum adalah 4x+3y= 550.
Source: ahmadcepatpintar.blogspot.com
Penyelesaiannya opimumnya ialah titik singgung tersebut. Setelah diperoleh daerah himpunan penyelesaian pada Jadi, z = f (x, y) = 200x + 300y f (125,225) = 200(125) + 300(225) = 25.000 + 67.500 = 92.500 jadi, laba maksimum yang diperoleh pedagang tersebut adalah rp 92.500,00 Jika bentuk umum fungsi tujuan dinotasikan dengan z = f ( x, y) = a x + b y maka bentuk umum garis selidik dinotasikan dengan a x + b y = k, dengan k ∈ r dimana k sembarang bilangan yang kita pilih. Ingat bahwa kendala ini berbentuk sistem pertidaksaam linear dengan dua variabel.
Source: brainly.co.id
Metode garis selidik adalah sebuah metode yang umum digunakan dalam program linear untuk menentukan nilai optimum dari suatu persoalan linear. Jika garis selidik yang melalui titik singgung berada paling dekat. Untuk titik (140,0) diperoleh z = 280 maka persamaan garis selidik pertama adalah. F(x,y) = px + qy. Contoh soal program linear metode garis selidik.
Source: ukurandansatuan.com
Nilai optimum akan mencapai salah satu titik ekstrim (titik sudut) di tempat garis selidik itu menyinggung. Nilai z diberikan sembarang nilai. Cara menentukan nilai optimum dapat menggunakan metode: Metode garis selidik adalah sebuah metode yang umum digunakan dalam program linear untuk menentukan nilai optimum dari suatu persoalan linear. Tentukan garis selidik ax + by = k apabila fungsi objektifnya f(x, y) = ax + by, a, b, dan k bilangan real.
Source: edukasi.lif.co.id
Jika bentuk umum fungsi tujuan dinotasikan dengan z = f ( x, y) = a x + b y maka bentuk umum garis selidik dinotasikan dengan a x + b y = k, dengan k ∈ r dimana k sembarang bilangan yang kita pilih. Cara menentukan nilai optimum dapat menggunakan metode: Tentukan garis selidik ax + by = k apabila fungsi objektifnya f(x, y) = ax + by, a, b, dan k bilangan real. Tentukan garis selidik ax + by = k apabila. Kemudian, kita lukis pada bidang koordinat dan.
Source: maretong.com
Tentukan daerah penyelesaian yang sesuai. Jadi, z = f (x, y) = 200x + 300y f (125,225) = 200(125) + 300(225) = 25.000 + 67.500 = 92.500 jadi, laba maksimum yang diperoleh pedagang tersebut adalah rp 92.500,00 Garis selidik adalah garis fungsi tujuan yang digeser secara sejajar. Nilai optimum dengan garis selidik. Perhatikan bahwa garis selidik yang menyebabkan fungsi objektif maksimum adalah 4x+3y= 550.
Source: brainly.co.id
Perhatikan bahwa garis selidik yang menyebabkan fungsi objektif maksimum adalah 4x+3y= 550. Tentukan model pertidaksamaan dari informasi soal dan gambarkan daerah selesaian dari sistem pertidaksamaan tersebut pada bidang koordinat. Dalam program linear terdapat sebuah fungsi linear yang disebut fungsi objektif atau fungsi tujuan, yang biasanya ditulis dalam bentuk $z = ax + by$ atau $f(x, y) = ax + by$. Nurman karim september 08, 2021 0. Penyelesaiannya opimumnya ialah titik singgung tersebut.
Source: maretong.com
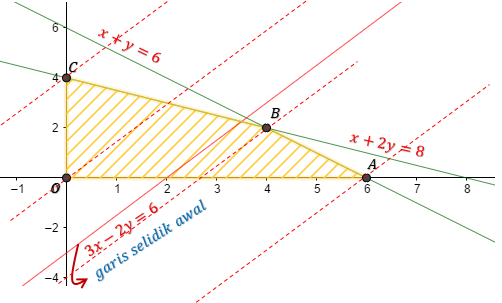
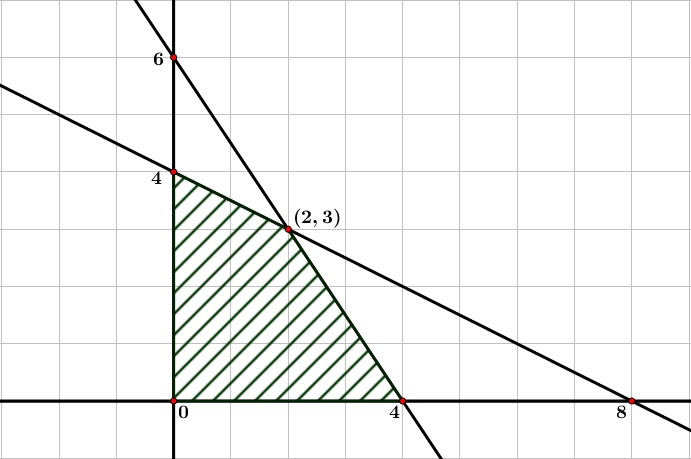
Jadi, diperoleh titik potong koordinat (0, 6) dan (4, 0). Tentukan model pertidaksamaan dari informasi soal dan gambarkan daerah selesaian dari sistem pertidaksamaan tersebut pada bidang koordinat. Menyelidiki nilai optimum fungsi objektif dengan dua acara yaitu : Kita akan cek nilai optimum fungsi obyektif dengan metode garis selidik. Membandingkan nilai fungsi objektif tiap titik ekstrim;
Source: piramidapascal.blogspot.com
Tentukan garis selidik ax + by = k apabila. Metode uji titik pojok dan b. Setelah diperoleh daerah himpunan penyelesaian pada Gambarlah grafik himpunan penyelesaian dari kendala dalam suatu masalah program linear. Menyelidiki nilai optimum fungsi objektif dengan dua acara yaitu :
Source: python-belajar.github.io
Namun diatara ketiga metode tersebut, yang paling mudah dan yang paling sering diajarkan adalah metode yang pertama yaitu metode uji titik pojok. Nilai optimum dengan garis selidik. Untuk mempermudah, ambil k = ab; Nurman karim september 08, 2021 0. Jika garis selidik yang melalui titik singgung berada paling dekat.
Source: smpn6gnkencana.sch.id
Dengan mengalikan kedua ruas persamaan garis selidik dengan 10.000, kamu mendapatkan nilai maksimum fungsi objektif. Garis selidik adalah garis fungsi tujuan yang digeser secara sejajar. Jika bentuk umum fungsi tujuan dinotasikan dengan z = f ( x, y) = a x + b y maka bentuk umum garis selidik dinotasikan dengan a x + b y = k, dengan k ∈ r dimana k sembarang bilangan yang kita pilih. Kita akan cek nilai optimum fungsi obyektif dengan metode garis selidik. Nilai optimum (nilai maksimum atau minimum) dari fungsi tujuan f(x, y) = ax + by dapat ditentukan dengan menggunakan metode grafik yang meliputi metode uji titik pojok dan garis selidik.
Source: yuksinau.id
Untuk titik (140,0) diperoleh z = 280 maka persamaan garis selidik pertama adalah. F(x,y) = px + qy. Garis selidik yang digunakan adalah axx +byy =ab, dengan ab œ[. Nilai optimum (nilai maksimum atau minimum) dari fungsi tujuan f(x, y) = ax + by dapat ditentukan dengan menggunakan metode grafik yang meliputi metode uji titik pojok dan garis selidik. Menentukan nilai optimum program linier dengan metode garis selidik.
Source: python-belajar.github.io
Soal 38 nilai optimum (program linear). Untuk lebih jelasnya, dibawah ini diberikan beberapa contoh soal nilai optimum dan pembahasannya. Menyelidiki nilai optimum fungsi objektif dengan dua acara yaitu : Metode uji titik pojok dan b. Kita akan cek nilai optimum fungsi obyektif dengan metode garis selidik.
Source: defantri.com
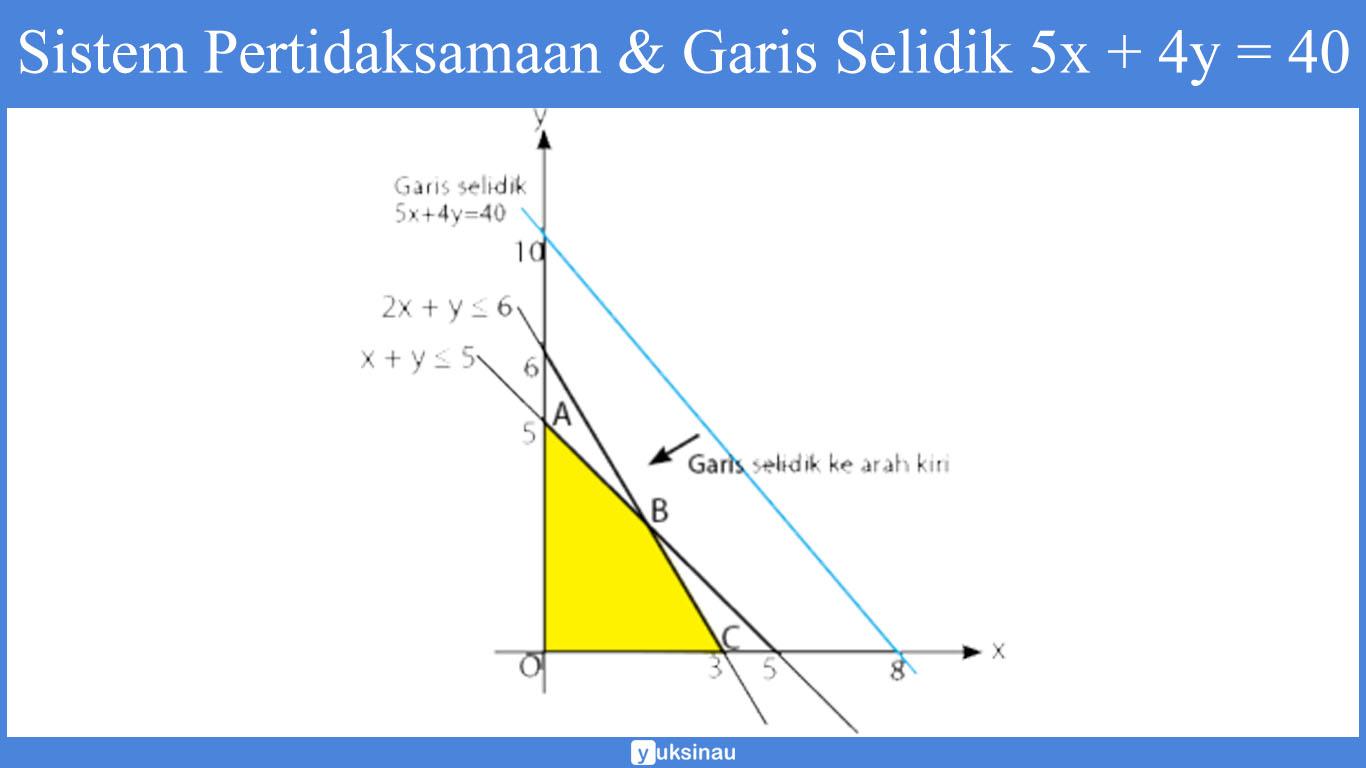
Dengan mengalikan kedua ruas persamaan garis selidik dengan 10.000, kamu mendapatkan nilai maksimum fungsi objektif. Membandingkan nilai fungsi objektif tiap titik ekstrim; Garis selidik diperoleh dari fungsi objektif f(x, y) = ax + by dimana garis selidiknya adalah. Menentukan nilai optimum dari fungsi tujuan dengan metode garis selidik y 350 300 (125,225) x 0 350 500 16x+25y=2.000 12. Jadi, z = f (x, y) = 200x + 300y f (125,225) = 200(125) + 300(225) = 25.000 + 67.500 = 92.500 jadi, laba maksimum yang diperoleh pedagang tersebut adalah rp 92.500,00
Source: youtube.com
Penyelesaiannya opimumnya ialah titik singgung tersebut. Berikut ini adalah cara menentukan nilai optimum dengan menggunakan metode garis selidik. Jika garis selidik yang melalui titik singgung berada paling jauh dari titik o(0,0), maka fungsi tujuan yang dicapai ialah nilai maksimum. Ingat bahwa kendala ini berbentuk sistem pertidaksaam linear dengan dua variabel. Metode garis selidik adalah sebuah metode yang umum digunakan dalam program linear untuk menentukan nilai optimum dari suatu persoalan linear.
Source: defantri.com
Jadi, diperoleh titik potong koordinat (0, 6) dan (4, 0). Suatu titik dalam poligon dimana f mencapai nilai maksimum atau minimum dinamakan penyelesaian optimum. Intinya, cara yang dapat dilakukan untuk mencari nilai optimum dengan garis selidik yang diperoleh dari persamaan fungsi objektif atau fungsi tujuannya. Kita akan cek nilai optimum fungsi obyektif dengan metode garis selidik. Tentukan daerah penyelesaian yang sesuai.
Source: python-belajar.github.io
Jika garis selidik yang melalui titik singgung berada paling jauh dari titik o(0,0), maka fungsi tujuan yang dicapai ialah nilai maksimum. Setelah diperoleh daerah himpunan penyelesaian pada Untuk menentukan nilai optimum suatu soal cerita yang berkaitan dengan progrma linear, ada tiga metode yang bisa kita gunakan yaitu metode uji titik pojok, metode garis selidik, dan metode gradien. Metode uji titik pojok dan b. Gambarlah grafik himpunan penyelesaian dari kendala dalam suatu masalah program linear.
Source: brainly.co.id
Jadi, diperoleh titik potong koordinat (0, 6) dan (4, 0). Nilai optimum akan mencapai salah satu titik ekstrim (titik sudut) di tempat garis selidik itu menyinggung. Tentukan garis selidik ax + by = k apabila fungsi objektifnya f(x, y) = ax + by, a, b, dan k bilangan real. Selain metode uji titik pojok, cara lain yang dapat digunakan untuk mengetahui nilai optimum adalah metode garis selidik. Metode garis selidik adalah sebuah metode yang umum digunakan dalam program linear untuk menentukan nilai optimum dari suatu persoalan linear.
This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site beneficial, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title menentukan nilai optimum dengan garis selidik by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
