Mencari Luas Daerah Yang Diarsir Integral. Luas daerah pertama, sebut saja l 1, berada di antara x = −2 dan x = 0. Menentukan luas daerah yang terletak dibatasi kurva y f. Tentukan luas daerah yang diarsir berikut jawab : Langkah pertama, mencari titik dasar.
Cara Mencari Luas Daerah Yang Diarsir Pada Segitiga Dengan From kitabelajar.github.io
132 o c2772 o d. Mencari selisih untuk menemukan luas daerah yang diarsir. Berdasarkan perhitungan integral tertentu, tentukan luas daerah yang diarsir di bawah kurva berikut ini: Batas bawah integral tentunya adalah a = lim n → ∞ x 1 = lim n → ∞ 1 n = 0, sedangkan batas atas integral tentunya adalah b = lim n → ∞ x 2 n = lim n → ∞ 2 = 2. Luas arsiran = 3 ∫ 1f(x)dx = 3 ∫ 1(4x − x2)dx = [2x2 − 1 3x3]31 = [2.32 − 1 3.33] − [2.12 − 1 3.13] = [18 − 9] − [2 − 1 3] = 71 3. Menentukan luas daerah yang terletak dibatasi kurva y fx dan sumbu x.
Menentukan luas daerah yang diarsir;
Bentuk daerah jenis 2 c) rumus cepat mencari luas rumus cepat tidak berlaku untuk seluruh daerah ya, quipperian. Tentukan luas daerah yang diarsir pada gambar berikut dengan menggunakan integral. Artinya, untuk mendapatkan luas daerah tersebut kita harus melakukan integral dua kali. Daerah yang diarsir pada gambar di atas terbagi menjadi dua. L 1 = ∫ 1 0 ( x + 3 − x 2) d x = [ 1 2 x 2 + 3 x − 1 3 x 3] 1 0 = 1 2 + 3 − 1 3 = 19 6. Gambar dulu kurva dan arsiran daerah yang dimaksud;
Source: mathcyber1997.com
Sebab menghitung luas daerah yang diarsir ini tak memiliki rumus pasti selain mengandalkan hitungan selisih. Tentukan luas daerah yang diarsir pada gambar gambar dibawah ini. Tolong dong yang bisa tentukan luas daerah arsiran pada bangun berikut a b c sama d pake brainly co id. Mencari luas daerah yang dibatasi kurva aplikasi integral dapat ditemukan pada cara mencari luas daerah yang dibatasi kurva. Menentukan luas daerah yang diarsir;
Source: ilmupenerangku.blogspot.com
Tentukan luas daerah yang dibatasi kurva x=y², x=y+2, y>=0. Luas antara dua kurva secara umum, penyelesaian luas daerah dengan menggunakan integral tentu selalu Batas bawah integral tentunya adalah a = lim n → ∞ x 1 = lim n → ∞ 1 n = 0, sedangkan batas atas integral tentunya adalah b = lim n → ∞ x 2 n = lim n → ∞ 2 = 2. Untuk mendapatkan luas daerah yang dibatasi kurva, dapat diperoleh dengan membagi luas daerah menjadi beberapa bagian. Pada artikel ini kita akan mempelajari cara cepat menghitung luas daerah berkaitan integral.
Source: ilmupenerangku.blogspot.com
Selanjutnya kita akan mencari luas daerah tersebut. Contoh soal integral luas daerah dan pembahasannya pdf bagikan contoh from bagikancontoh.blogspot.com. Cara integral inilah yang dipelajari pada tingkat kelas xii ipa. Menentukan luas daerah yang diarsir : Tentukan luas daerah yang diarsir pada gambar gambar dibawah ini.
Source: contohsoalunbk-04.blogspot.com
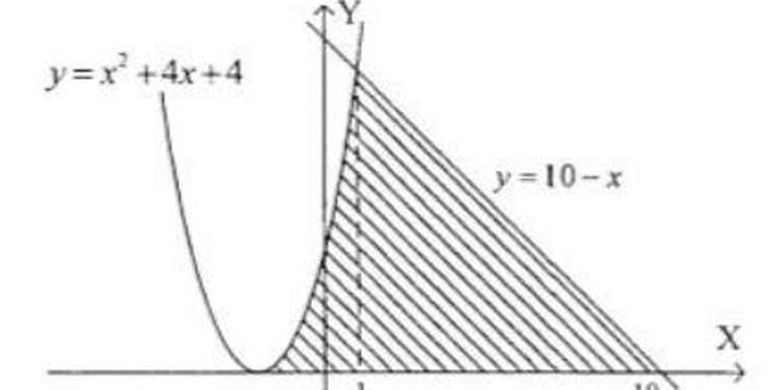
21 contoh soal integral mencari luas daerah. L 2 adalah daerah yang dibatasi oleh garis y = 4 dan kurva y = x 2. L 1 adalah daerah yang dibatasi oleh kurva y = x 2 dan garis y = x + 3: Jika dilihat dari parabola y 2x 2 8x 6 daerah yang diarsir ada yang di bawah parabola dan dan di atas parabola. Daerah r dibatasi oleh y y ax2 untuk x 02.
Source: kuncisoallengkap.blogspot.com
21 contoh soal integral mencari luas daerah. Cara menghitung luas daerah yang diarsir dapat dilakukan dengan rumus kombinasi yang berasal dari beberapa bangun datar. Sehingga luas daerah u dapat dihitung dengan rumus. Di akhir segmen ketiga, diajukan pertanyaan sebagai berikut: Luas daerah yang diarsir adalah.
Source: kitabelajar.github.io
Menentukan luas daerah yang terletak dibatasi kurva y f. Cara yang sama dapat kita gunakan untuk menentukan luas daerah yang terletak di bawah sumbu x. Fungsinya adalah y 4 x2 rightarrow x sqrt4 y. Langkah kedua, mencari titik potong. Menentukan luas daerah yang terletak dibatasi kurva y f.
Source: contohsoalitu.blogspot.com
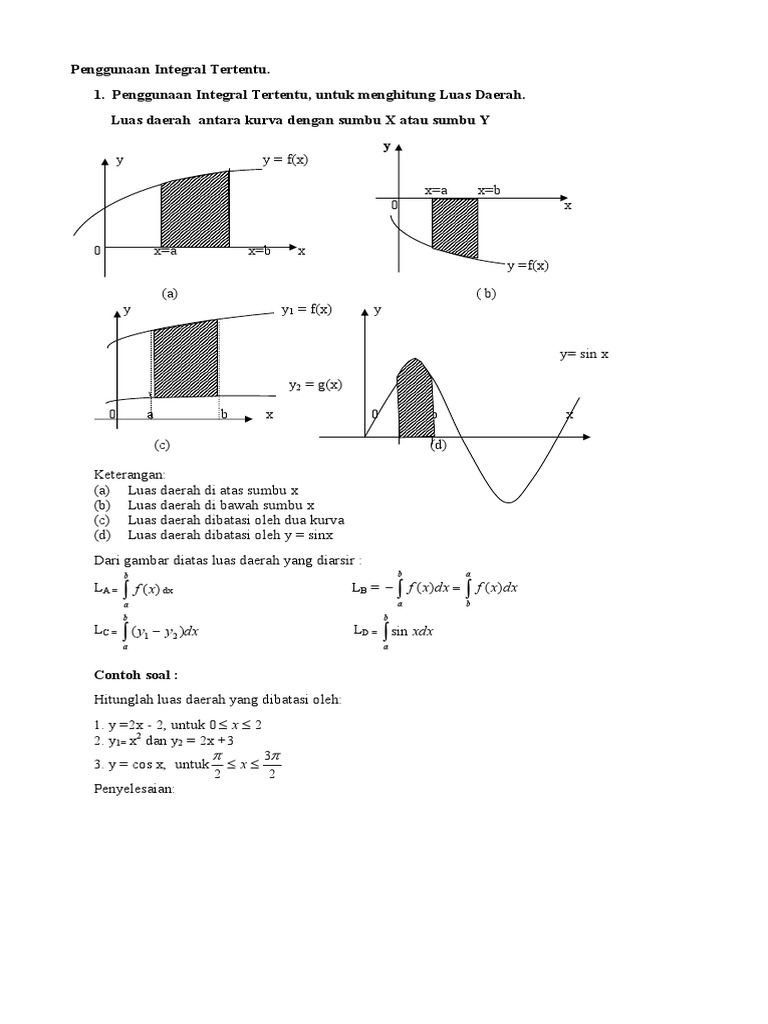
Jadi, luas daerah yang diarsir adalah 71 3 satuan luas. Jika dilihat dari parabola y 2x 2 8x 6 daerah yang diarsir ada yang di bawah parabola dan dan di atas parabola. Pada bagian yang diarsir, kurva f(x) lebih di atas dibandingkan dengan kurva g(x) maka luas daerah di atas bisa dinyatakan dengan Nilai integral a di atas pastilah negatif a. Integral tak tentu adalah bentuk integral yang hasilnya berupa fungsi dalam variabel tertentu dan masih memuat konstanta integrasi.
Source: kompas.com
21 contoh soal integral mencari luas daerah. Carilah luas kurva di antara garis x0 x4 dan sumbu x. Selain itu aplikasi integral juga digunakan untuk mencari volume benda putar yang merupakan daerah yang dibatasi kurva kemudian diputar 360 o. Cara menghitung luas daerah yang diarsir dapat dilakukan dengan rumus kombinasi yang berasal dari beberapa bangun datar. Artinya, untuk mendapatkan luas daerah tersebut kita harus melakukan integral dua kali.
Source: dapatkancontoh.blogspot.com
Luas daerah yang diarsir pada gambar di atas dapat dinyatakan dengan rumus. Daerah r dibatasi oleh y y ax2 untuk x 02. Integral tak tentu adalah bentuk integral yang hasilnya berupa fungsi dalam variabel tertentu dan masih memuat konstanta integrasi. Luas daerah yang diarsir adalah. Tentukan luas daerah yang diarsir pada gambar berikut dengan menggunakan integral.
Source: sebutkanitu.blogspot.com
Sekian pembahasan mengenai materi aplikasi integral untuk menentukan luas daerah yang dibatasi. Menentukan luas daerah yang terletak dibatasi kurva y fx dan sumbu x. Berdasarkan perhitungan integral tertentu, tentukan luas daerah yang diarsir di bawah kurva berikut ini: L 1 = ∫ 1 0 ( x + 3 − x 2) d x = [ 1 2 x 2 + 3 x − 1 3 x 3] 1 0 = 1 2 + 3 − 1 3 = 19 6. Nilai integral a di atas pastilah negatif a.
Source: kitabelajar.github.io
Tolong dong yang bisa tentukan luas daerah arsiran pada bangun berikut a b c sama d pake brainly co id. Tentukan luas daerah yang diarsir pada gambar berikut dengan menggunakan integral. Untuk siswa sma, dijelaskan mengenai integral. Salah satu penerapan penting dari integral yaitu untuk mencari luas suatu bidang dengan bentuk yang tidak beraturan. Sehingga, luas daerah yang dibatasi integral dapat dicari melalui persamaan berikut.
Source: brainly.co.id
Untuk siswa sma, dijelaskan mengenai integral. Mencari luas daerah yang dibatasi kurva aplikasi integral dapat ditemukan pada cara mencari luas daerah yang dibatasi kurva. Bentuk daerah jenis 2 c) rumus cepat mencari luas rumus cepat tidak berlaku untuk seluruh daerah ya, quipperian. Berdasarkan perhitungan integral tertentu, tentukan luas daerah yang diarsir di bawah kurva berikut ini: Jika dilihat dari parabola y 2x 2 8x 6 daerah yang diarsir ada yang di bawah parabola dan dan di atas parabola.
Source: kitabelajar.github.io
Tentukan luas daerah yang dibatasi kurva x=y², x=y+2, y>=0. Batas bawah integral tentunya adalah a = lim n → ∞ x 1 = lim n → ∞ 1 n = 0, sedangkan batas atas integral tentunya adalah b = lim n → ∞ x 2 n = lim n → ∞ 2 = 2. Tentukan luas daerah yang diarsir berikut jawab : X = y − 3 → y = x + 3. Contoh soal dan pembahasan tentang luas daerah dengan integral.
Source: youtube.com
Perhatikan bahwa dari selang ( 0, 4), kurva y = 6 x − x 2 selalu berada di atas kurva y = x 2 − 2 x. Cara integral inilah yang dipelajari pada tingkat kelas xii ipa. L 1 adalah daerah yang dibatasi oleh kurva y = x 2 dan garis y = x + 3: Tentukanlah luas yang dibentuk oleh y = sin x, y = 1, x = 0 dan terletak di kuadran 1. X = y − 3 → y = x + 3.
Source: kuncisoallengkap.blogspot.com
Cara menghitung luas daerah yang diarsir dapat dilakukan dengan rumus kombinasi yang berasal dari beberapa bangun datar. Hitunglah luas daerah yang diarsir. Mencari luas daerah yang diarsir dengan integral halaman all. Partisikan untuk mencari luas daerah yang diarsir : Contoh soal integral luas daerah dibawah sumbu x.
Source: teamhannamy.blogspot.com
Mencari selisih untuk menemukan luas daerah yang diarsir. Karena luas berupa bilangan tak negatif, a kita kalikan dengan negatif sehingga menjadi tak negatif. Fungsinya adalah y 4 x2 rightarrow x sqrt4 y. L 1 adalah daerah yang dibatasi oleh kurva y = x 2 dan garis y = x + 3: Sekian pembahasan mengenai materi aplikasi integral untuk menentukan luas daerah yang dibatasi.
Source: kitabelajar.github.io
21 contoh soal integral mencari luas daerah. Gambar dulu kurva dan arsiran daerah yang dimaksud; Daerah l 1 bernilai negatif karena berada di bawah sumbu x. Daerah yang diarsir pada gambar di atas terbagi menjadi dua. Sehingga luas daerah u dapat dihitung dengan rumus.
Source: kitabelajar.github.io
Luas daerah yang diarsir adalah. Contoh soal integral luas daerah dan pembahasannya pdf bagikan contoh from bagikancontoh.blogspot.com. Cara integral inilah yang dipelajari pada tingkat kelas xii ipa. Dengan demikian, integral tentu yang dinyatakan oleh jumlah riemann tersebut adalah ∫. Luas daerah yang diarsir adalah.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site serviceableness, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title mencari luas daerah yang diarsir integral by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
