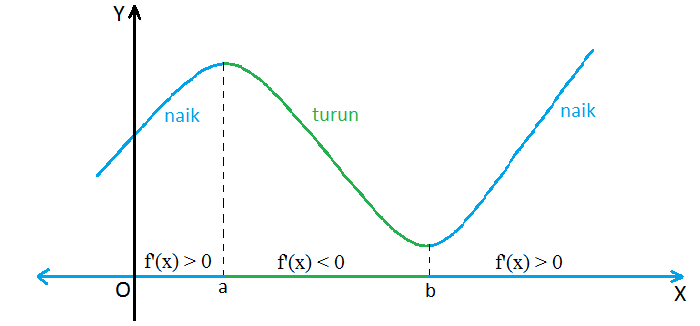
Fungsi Naik Dan Turun. Hg* (*itb bandung) ma3231 analisis real 13 march 2017 3 / 22. Fungsi f(x) dikatakan turun jika f'(x) < 0 fungsi f(x) dikatakan stasioner jika f'(x) = 0 fungsi f(x) dikatakan tidak naik jika f'(x) ≤ 0 fungsi f(x) dikatakan tidak turun jika f'(x) ≥ 0. (1) jika f (x) adalah fungsi naik pada interval a maka f’ (x) > 0, untuk setiap x ϵ a. Jika fungsi f continue dan terdiferensial kan dalam interval l , maka :
Soal dan Penyelesaian Fungsi Naik dan Fungsi Turun YouTube From youtube.com
Fungsi naik dan fungsi turun. Turunan hasil kali dan hasil bagi dua fungsi. Untuk lebih jelasnya, dibawah ini diberikan 10 contoh soal fungsi naik & fungsi turun dan penyelesaiannya / pembahasannya. Contoh soal fungsi naik dan fungsi turun. Kompetensi dasar 3.3 selamat belajar. Turunan pertama f' (x) memberi kita kemiringan dari garis singgung pada grafik f di titik x.
Jadi f (x) naik pada interval x > 3 dan turun pada interval x < 3.
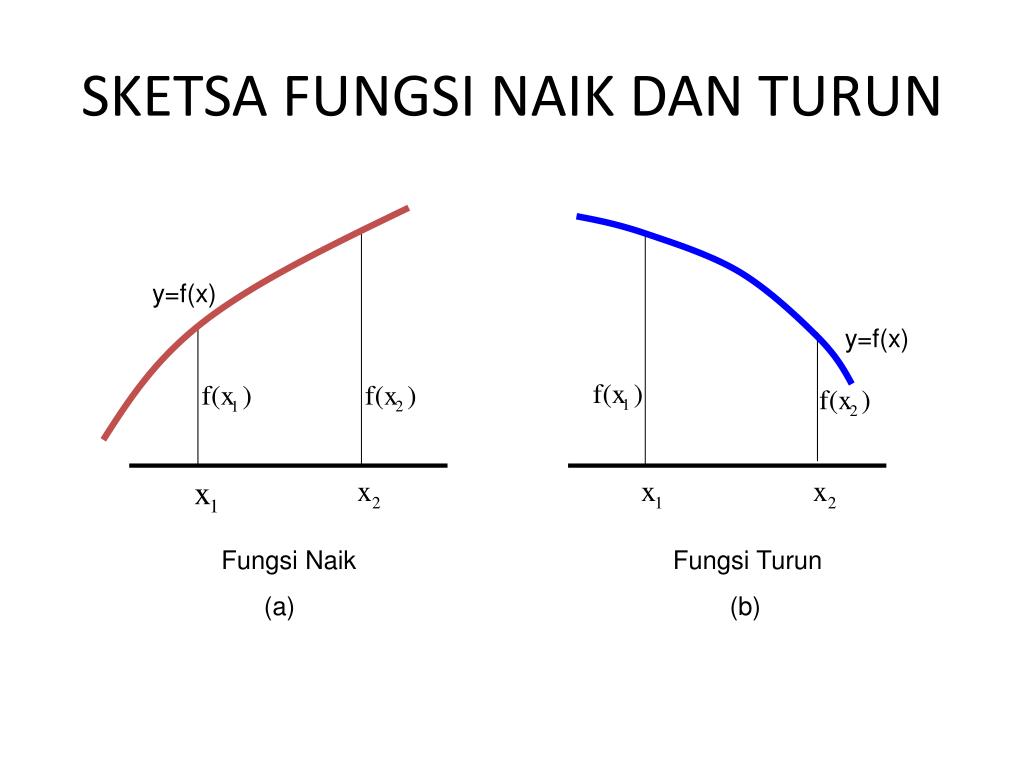
Fungsi f f naik pada interval tersebut jika f (x1) < f (x2) f ( x 1) < f ( x 2) bilamana x1 < x2 x 1 < x 2. Untuk memahami materi ini, anda harus mempelajari materi turunan fungsi. Fungsi f dikatakan turun (decreasing) pada i jika untuk setiap pasangan bilangan x1 dan x2 di i berlaku: Jika f (x) = x 2 − 6x + 8, tentukan interval f (x) naik dan interval f (x) turun! Fungsi naik, fungsi turun, dan fungsi diam (stasioner) merupakan kondisi dari turunan pertama suatu fungsi pada suatu interval tertentu. Fungsi naik dan fungsi turun jika kita menggambar kurva dari kiri ke kanan arahnya naik, maka grafik fungsinya naik, tapi bila arahnya turun maka grafik fungsinya turun.
Source: youtube.com
Ini juga berkaitan dengan fakta bahwa m = f' (x) kedua teorema di atas memberi kita cara yang meyakinkan untuk menentukan selang kemonotonan sebuah. Jika f ′ ( x) bertanda positif, atau f ′ ( x) > 0, maka kurva fungsi dalam keadaan naik (disebut. Jika x1 < x2, maka f(x1) > f(x2). Y = 5t + 10t2; Fungsi f (x) = 2x 3 − 3x 2 − 36x naik pada.
Source: konsep-matematika.com
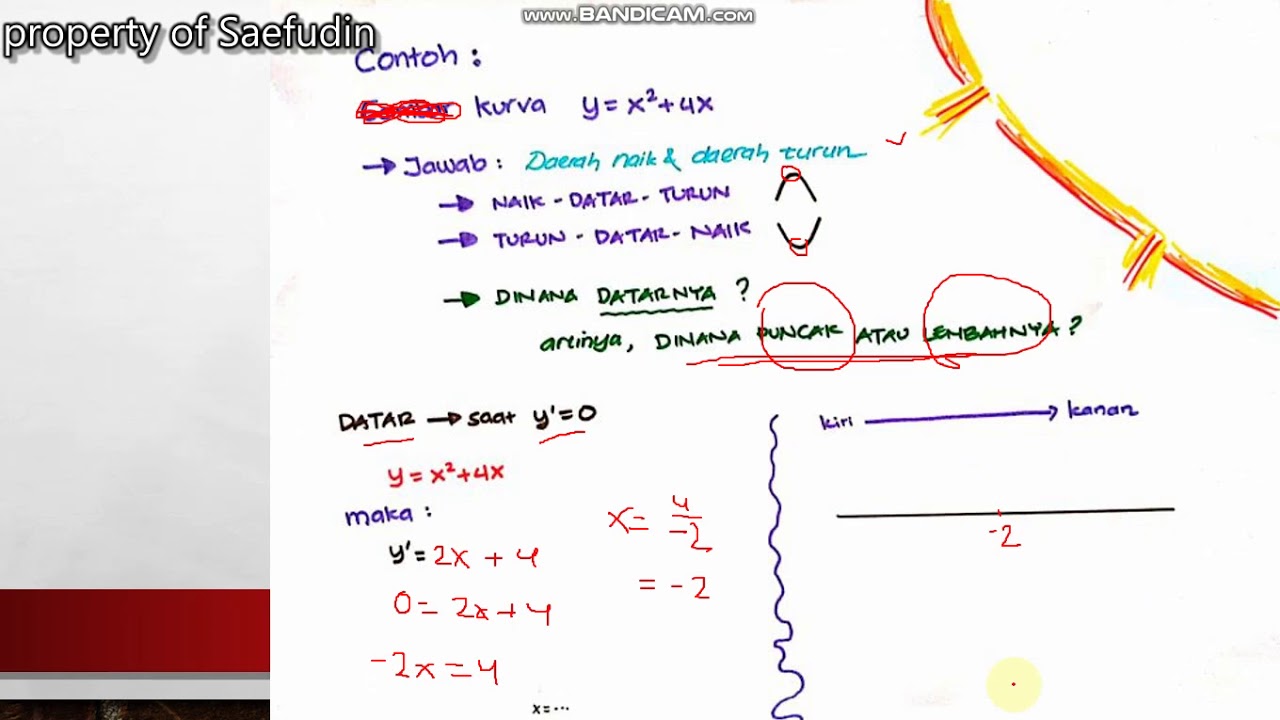
Hasil ini kemudian diubah menjadi persamaan sama dengan nol, sehingga: Fungsi naik dan fungsi turun. Fungsi naik dan fungsi turun. Jika f' (x) > 0, garis singgung naik, jika f' (x) < 0, garis singgung turun. Jika fungsi f continue dan terdiferensial kan dalam interval l , maka :
Source: youtube.com
Artinya bahwa fungsi tidak memilik interval fungsi naik. Z = 3t2 + 6t + 5 contoh: Contoh soal fungsi naik dan fungsi turun. Fungsi f f naik pada interval tersebut jika f (x1) < f (x2) f ( x 1) < f ( x 2) bilamana x1 < x2 x 1 < x 2. Hg* (*itb bandung) ma3231 analisis real 13 march 2017 3 / 22.
Source: youtube.com
Pertidaksamaan diatas akan terpenuhi jika < 0 sementara tidak akan pernah bernilai negatif. Turunan ini sudah dibahas di postingan sebelumnya. (1) jika f (x) adalah fungsi naik pada interval a maka f’ (x) > 0, untuk setiap x ϵ a. Untuk memahami materi ini, anda harus mempelajari materi turunan fungsi. Fungsi naik atau turun disebut fungsi monoton.
Source: dikdasmen.my.id
Fungsi naik dan fungsi turun. Sebagai contoh akan diuraikan pada soal berikut ini. Grafik fungsi fx x³3x² 9x 1 turun pada interval brainlycoid. Contoh dan contoh soal fungsi naik fungsi turun dan nilai stasioner fungsi naik fungsi turun dan fungsi diam stasioner merupakan kondisi dari turunan pertama suatu fungsi pada suatu interval tertentu. Fungsi naik dan fungsi turun y a (maks) c (titik belok) y = f(x) b (min).
Source: youtube.com
11.1 de nisi dan limit fungsi monoton contoh 1. Fungsi naik dan fungsi turun. Fungsi f (x) = 2x 3 − 3x 2 − 36x naik pada. Satu potong dibentuk lingkaran dan potongan kedua bujur sangkar. Jadi f (x) naik pada interval x > 3 dan turun pada interval x < 3.
Source: youtube.com
Fungsi naik dan fungsi turun y a (maks) c (titik belok) y = f(x) b (min). Kondisi yang dimaksud dapat berupa berikut. Fungsi dikatakan monoton naik pada interval i jika untuk x1 < x2 , ∀ x1 , x2 ϵ i fungsi dikatakan monoton turun pada interval i jika untuk x1 < x2 , ∀ x1 , x2 ϵ i 1 2( ) ( )f x f x< 1 2( ) ( )f x f x> ( )f x ( )f x 4. Contoh dan contoh soal fungsi naik fungsi turun dan nilai stasioner fungsi naik fungsi turun dan fungsi diam stasioner merupakan kondisi dari turunan pertama suatu fungsi pada suatu interval tertentu. Turunan ini sudah dibahas di postingan sebelumnya.
Source: youtube.com
Pembahasan mathematics4us kali ini membahas mengenai kelanjutan materi turunan yaitu fungsi naik dan fungsi turun, serta nilai stasioner. Jika fungsi f continue dan terdiferensial kan dalam interval l , maka : Suatu fungsi dikatakan naik jika x bergerak ke kanan, grafik fungsi tersebut bergerak ke atas, dan turun jika grafik fungsi tersebut bergerak ke bawah. 11.1 de nisi dan limit fungsi monoton contoh 1. Fungsi yang naik dan turun sekaligus pada hmestilah konstan pada h.
Source: fr.slideshare.net
Fungsi naik, fungsi turun, dan fungsi diam (stasioner) merupakan kondisi dari turunan pertama suatu fungsi pada suatu interval tertentu. Fungsi dikatakan monoton naik pada interval i jika untuk x1 < x2 , ∀ x1 , x2 ϵ i fungsi dikatakan monoton turun pada interval i jika untuk x1 < x2 , ∀ x1 , x2 ϵ i 1 2( ) ( )f x f x< 1 2( ) ( )f x f x> ( )f x ( )f x 4. (1) jika f (x) adalah fungsi naik pada interval a maka f’ (x) > 0, untuk setiap x ϵ a. Untuk tiap x € l. A = harga maksimum (pada x = x 1), karena harga y dititik ini lebih besar daripada y di kanan kirinya.
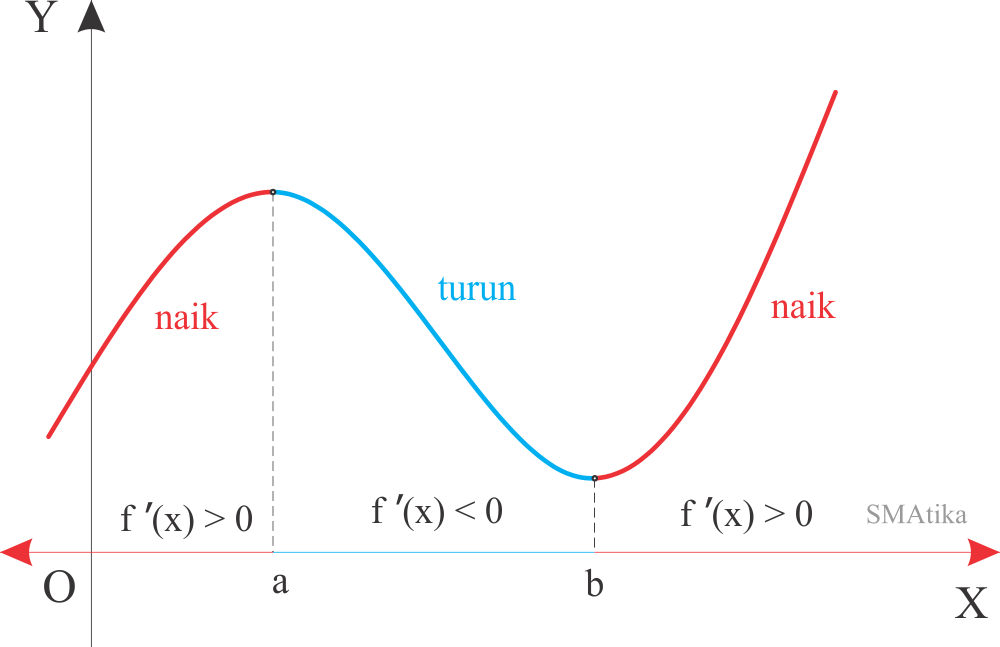Source: smatika.blogspot.com
Suatu fungsi dikatakan naik jika x bergerak ke kanan, grafik fungsi tersebut bergerak ke atas, dan turun jika grafik fungsi tersebut bergerak ke bawah. 0 x 1 x 2 x 3. Fungsi naik, fungsi turun, dan fungsi diam (stasioner) merupakan kondisi dari turunan pertama suatu fungsi pada suatu interval tertentu. Tetapi sebuah grafik biasanya digambar dengan memplot beberapa titik dan menghubungkan. Tentukan nilai x agar fungsi f(x) = x 2 — 8x — 9 naik.
Source: slideserve.com
Jika fungsi f continue dan terdiferensial kan dalam interval l , maka : Fungsi naik jika f '(x) > 0. Ini juga berkaitan dengan fakta bahwa m = f' (x) kedua teorema di atas memberi kita cara yang meyakinkan untuk menentukan selang kemonotonan sebuah fungsi, baik itu fungsi naik, maupun turun. R !r yang dide nisikan sebagai A = harga maksimum (pada x = x 1), karena harga y dititik ini lebih besar daripada y di kanan kirinya.
Source: slideserve.com
Kemonotonan grafik fungsi merupakan materi yang dibahas pada turunan dan aplikasi turunan. Hasil ini kemudian diubah menjadi persamaan sama dengan nol, sehingga: Fungsi naik dan fungsi turun. Fungsi f (x) = 2x 3 − 3x 2 − 36x naik pada. Jadi nilai f x dapat digambarkan pada selang interval di atas.
Source: teamhannamy.blogspot.com
Kondisi yang dimaksud dapat berupa berikut. Bagaimanakah persamaannya dalam bentuk implisit, eksplisit, dan A interval fungsi naik dan turun b koordinat titik stasioner c interval cekung atas dan cekung bawah d koordinat titik beloknya jawab fx x 3 6x 2 9x 5 fx 3x 2 12x 9 fx 6x 12. Fungsi naik, fungsi turun, dan fungsi konstan. Fungsi turun jika f '(x) < 0
Source: youtube.com
Suatu fungsi dikatakan naik jika x bergerak ke kanan, grafik fungsi tersebut bergerak ke atas, dan turun jika grafik fungsi tersebut bergerak ke bawah. Fungsi naik atau turun disebut fungsi monoton. Misalkan fungsi f f terdefinisi pada sebuah interval, dan andaikan x1 x 1 dan x2 x 2 menunjukkan titik pada interval tersebut. Untuk lebih jelasnya, dibawah ini diberikan 10 contoh soal fungsi naik & fungsi turun dan penyelesaiannya / pembahasannya. Tentukan interval fungsi naik dan fungsi turun dari.
Source: websiteedukasi.id
Turunan ini sudah dibahas di postingan sebelumnya. Z = 3t2 + 6t + 5 contoh: Tetapi sebuah grafik biasanya digambar dengan memplot beberapa titik dan menghubungkan. Fungsi naik atau turun disebut fungsi monoton. Artinya bahwa fungsi tidak memilik interval fungsi naik.
Source: slideshare.net
Misalkan a = {x│ a < x < b } maka berlaku. (2) jika f (x) adalah fungsi turun pada interval a maka f’ (x) < 0, untuksetiap x ϵ a. Fungsi naik dan fungsi turun y a (maks) c (titik belok) y = f(x) b (min). Jika f ′ ( x) bertanda positif, atau f ′ ( x) > 0, maka kurva fungsi dalam keadaan naik (disebut. Y = 5t + 10t2;
Source: youtube.com
Fungsi naik dan fungsi turun. Kemonotonan grafik fungsi merupakan materi yang dibahas pada turunan dan aplikasi turunan. Terimakasih sudah mengunjungi idschool (dot)net, semoga bermanfaat! (2) jika f (x) adalah fungsi turun pada interval a maka f’ (x) < 0, untuksetiap x ϵ a. Fungsi naik dan fungsi turun.
Source: youtube.com
Turunan pertama f' (x) memberi kita kemiringan dari garis singgung pada grafik f di titik x. Jadi nilai f x dapat digambarkan pada selang interval di atas. Mungkin kita berpikir untuk menggambar grafiknya dan mengamatinya. Fungsi f dikatakan monoton ketat (strictly monotonic) pada i jika f naik saja atau turun saja pada i. (3) jika f (x) adalah fungsi tidak naik pada.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site good, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title fungsi naik dan turun by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
