Distribusi Proporsi. Untuk pengambilan sampel dengan pengembalian rumus: Misalkan populasi 1 adalah n1 dan sampel 1 adalah n1 maka terdapat c (n1,n1) dengan proporsi p1. I i = pdrb atas dasar harga berlaku provinsi i; Misalnya terdapat 2 populasi binomial (populasi yang dibedakan menjadi 2 kelompok, seperti merokok dan tidak merokok, setuju dan tidak setuju, dsb) dengan ukuran n1 dan n2.
Contoh Soal Distribusi Sampling Proporsi Kunci Ujian From kunciujianbaru.blogspot.com
Pengantar populasi adalah seluruh obyek yang diteliti mengumpulkan informasi dari populasi disebut sensus , dari sini diperoleh parameter 3 Probabilitas terjadinya suatu peristiwa θ : Pengujian dua proporsi digunakan ketika akan membandingkan apakah proporsi pada populasi pertama lebih kecil, sama atau lebih besar dibandingkan proporsi pada populasi kedua. Secara umum pengertian distribusi binomial dapat ditulis seperti di atas. Maka didapat parameter proporsi a sebesar µ = (y/n). Dist i = distribusi pdrb provinsi i;
Untuk pengambilan sampel tanpa pengembalian rumus:
Distribusi binomial adalah distribusi sampling dari proporsi proporsi yang mungkin kita amati dalam sampel sampel random yang ditarik dari suatu populasi yang terdiri dari kelas. Menunjukkan struktur perekonomian atau peranan wilayah dalam perekonomian negara. Populasi bank, populasi perusahaan reksa dana, dsb. Distribusi sampling dari statistik tersebut. Sampel dan distribusi sampling prof. Distribusi binomial adalah distribusi sampling dari proporsi proporsi yang mungkin kita amati dalam sampel sampel random yang ditarik dari suatu populasi yang terdiri dari kelas.
Source: slideshare.net
I i = pdrb atas dasar harga berlaku provinsi i; Misalkan populasi 1 adalah n1 dan sampel 1 adalah n1 maka terdapat c (n1,n1) dengan proporsi p1. Misalkan populasi diketahui berukuran n yang didalamnya didapat peristiwa a sebanyak y di antara n. Distribusi sampling proporsi dapat digunakan untuk mengetahui persentase atau perbandingan antara dua hal yang berkomplemen (peristiwa binomial), seperti persentase perokok dan bukan perokok, persentase pemilih dan bukan pemilih di suatu pemilu, dan perbandingan antara pemakai dan bukan pemakai hasil produksi tertentu. Untuk ini diperlukan sebuah teori yang dikenal dengan nama distribusi sampling.
Source: slideserve.com
Maka didapat parameter proporsi peristiwa a sebesar = (y/n) dari populasi diambil sampel acak berukuran n dan dimisalkan didalamnya ada peristiwa a sebanyak x. Sebagai contoh, total mahasiswa adalah 100 orang, jika 30 mahasiswa diantaranya merokok, proporsi mahasiswa yang merokok adalah 30/100 atau 30%. Logika yang digunakan dalam estimasi proporsi populasi sama dengan ketika kita membangun rumus estimasi mean populasi. Maka didapat parameter proporsi a sebesar µ = (y/n). Pengujian dua proporsi digunakan ketika akan membandingkan apakah proporsi pada populasi pertama lebih kecil, sama atau lebih besar dibandingkan proporsi pada populasi kedua.
Source: youtube.com
Pengujian dua proporsi digunakan ketika akan membandingkan apakah proporsi pada populasi pertama lebih kecil, sama atau lebih besar dibandingkan proporsi pada populasi kedua. Logika yang digunakan dalam estimasi proporsi populasi sama dengan ketika kita membangun rumus estimasi mean populasi. Maka didapat parameter proporsi peristiwa a sebesar = (y/n) dari populasi diambil sampel acak berukuran n dan dimisalkan didalamnya ada peristiwa a sebanyak x. Sampel ini memberikan statistik proporsi peristiwa a = x/n. Populasi bank, populasi perusahaan reksa dana, dsb.
Source: pdfslide.net
Distribusi sampling proporsi 25/07/15 19 adalah distribusi dari proporsi (presentase) yang diperoleh dari semua sampel sama besar yang mungkin dari satu populasi n x proporsi dari populasi p = n x proporsi dari sampel p = dapat digunakan untuk mengetahui perbandingan antara Distribusi sampling untuk proporsi sifat penaksir ( estimator ) titik estimasi interval ( interval estimation ) menguji ketepatan sampling. Distribusi sampling biasanya diberi nama bergantung pada nama statistik yang digunakan. Misalkan populasi 1 adalah n1 dan sampel 1 adalah n1 maka terdapat c (n1,n1) dengan proporsi p1. Materi ini sebenarnya telah banyak.
Source: slidetodoc.com
Π = proporsi kejadian sukses dari populasi yang diestimasi p = proporsi kejadian sukses dari sampel z = nilai distribusi normal Dist i = distribusi pdrb provinsi i; Misalkan, kita ingin menaksir m/n,. Secara ringkas, rumus estimasi proporsi π adalah sebagai berikut: Jika dalam sebiah populasi, π :
Source: rosinai-seat.blogspot.com
Tabel dua arah di bawah ini adalah rangkuman hasil penelitian yang mengamati hasil ujian nasional siswa di sebuah sekolah dasar. Misalkan populasi 1 adalah n1 dan sampel 1 adalah n1 maka terdapat c (n1,n1) dengan proporsi p1. Distribusi sampling dari statistik tersebut. Untuk pengambilan sampel dengan pengembalian rumus: Bayangkan kita memiliki sekelompok populasi.
Source: barisancontoh.blogspot.com
Untuk ini diperlukan sebuah teori yang dikenal dengan nama distribusi sampling. Populasi bank, populasi perusahaan reksa dana, dsb. Bayangkan kita memiliki sekelompok populasi. Untuk pengambilan sampel dengan pengembalian rumus: Distribusi sampling untuk proporsi sifat penaksir ( estimator ) titik estimasi interval ( interval estimation ) menguji ketepatan sampling.
Source: kunciujianbaru.blogspot.com
Distribusi binomial adalah distribusi sampling dari proporsi proporsi yang mungkin kita amati dalam sampel sampel random yang ditarik dari suatu populasi yang terdiri dari kelas. Tabel dua arah di bawah ini adalah rangkuman hasil penelitian yang mengamati hasil ujian nasional siswa di sebuah sekolah dasar. Distribusi sampling dari proporsi q untuk nilai n yang besar (n > 30), distribusi sampling proporsi mendekati suatu distribusi normal q sedangkan populasinya mengikuti distribusi binomial q perlu diperhatikan bahwa proporsi adalah variabel diskrit, sehingga diperlukan faktor koreksi (±1/2n ) dalam mengubahnya kedalam skor z untuk menentukan. Untuk ini diperlukan sebuah teori yang dikenal dengan nama distribusi sampling. Ketika kita mengambil sampel data, kita akan mendapatkan hasil bahwa terdapat berbagai perbedaan perhitungan dari satu sampel ke sampel lain.
Source: situsekonomi.com
Misalnya terdapat 2 populasi binomial (populasi yang dibedakan menjadi 2 kelompok, seperti merokok dan tidak merokok, setuju dan tidak setuju, dsb) dengan ukuran n1 dan n2. Untuk pengambilan sampel dengan pengembalian rumus: Populasi bank, populasi perusahaan reksa dana, dsb. Probabilitas terjadinya suatu peristiwa θ : Sedangkan populasi 2 adalah n2 dan.
Source: kunciujianbaru.blogspot.com
Distribusi sampling proporsi dapat digunakan untuk mengetahui persentase atau perbandingan antara dua hal yang berkomplemen (peristiwa binomial), seperti persentase perokok dan bukan perokok, persentase pemilih dan bukan pemilih di suatu pemilu, dan perbandingan antara pemakai dan bukan pemakai hasil produksi tertentu. Misalkan populasi diketahui berukuran n yang didalamnya didapat peristiwa a sebanyak y di antara n. Misalkan, kita ingin menaksir m/n,. Pengantar populasi adalah seluruh obyek yang diteliti mengumpulkan informasi dari populasi disebut sensus , dari sini diperoleh parameter 3 Pengujian dua proporsi digunakan ketika akan membandingkan apakah proporsi pada populasi pertama lebih kecil, sama atau lebih besar dibandingkan proporsi pada populasi kedua.
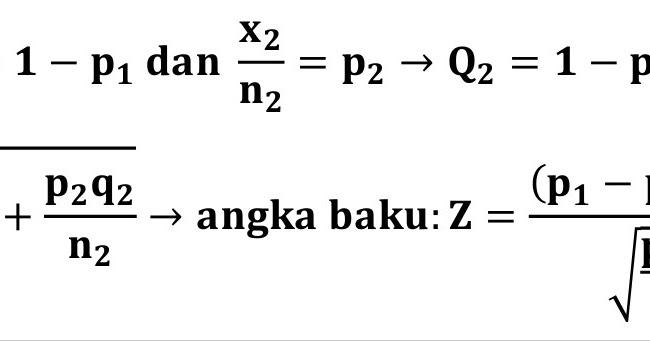Source: situsekonomi.com
Populasi bank, populasi perusahaan reksa dana, dsb. Misalkan populasi 1 adalah n1 dan sampel 1 adalah n1 maka terdapat c (n1,n1) dengan proporsi p1. Ukuran sampel di kedua grup harus mencukupi serta distribusinya diasumsikan mengikuti distribusi normal. Misalkan, kita ingin menaksir m/n,. Sedangkan populasi 2 adalah n2 dan.
Source: khalilqibran.blogspot.com
Dari populasi ini diambil sampel acak berukuran n dan dimisalkan didalamnya ada peristiwa a sebanyak x. Pengujian dua proporsi digunakan ketika akan membandingkan apakah proporsi pada populasi pertama lebih kecil, sama atau lebih besar dibandingkan proporsi pada populasi kedua. Bayangkan kita memiliki sekelompok populasi. Maka didapat parameter proporsi peristiwa a sebesar = (y/n) dari populasi diambil sampel acak berukuran n dan dimisalkan didalamnya ada peristiwa a sebanyak x. Sampel dan distribusi sampling prof.
Source: barucontohsoal.blogspot.com
Diperlukan proporsi sampel kejadian di grup 1 dan proporsi sampel kejadian di grup 2. Bayangkan kita memiliki sekelompok populasi. Misalkan populasi diketahui berukuran n yang didalamnya didapat peristiwa a sebanyak y di antara n. Misalkan, kita ingin menaksir m/n,. Semakin besar distribusi pdrb provinsi, semakin besar peranan provinsi tersebut dalam perekonomian nasional.
Source: jawabanbukunya.blogspot.com
Untuk ini diperlukan sebuah teori yang dikenal dengan nama distribusi sampling. I i = pdrb atas dasar harga berlaku provinsi i; Misalkan, kita ingin menaksir m/n,. Menunjukkan struktur perekonomian atau peranan wilayah dalam perekonomian negara. Distribusi sampling biasanya diberi nama bergantung pada nama statistik yang digunakan.
Source: slideshare.net
Populasi bank, populasi perusahaan reksa dana, dsb. Sampel ini memberikan statistik proporsi peristiwa a = x/n. Misalkan, kita ingin menaksir m/n,. Merupakan distribusi teoritis (distribusi kemungkinan) dari semua hasil sampel yang mungkin, dengan ukuran sampel yang tetap n, pada statistik (karakteristik sampel) yang digeneralisasikan ke populasi. Untuk pengambilan sampel tanpa pengembalian rumus:
Source: caripembahasannya.blogspot.com
Sampel dan distribusi sampling prof. Dari populasi ini diambil sampel acak berukuran n dan dimisalkan didalamnya ada peristiwa a sebanyak x. Distribusi sampling untuk proporsi sifat penaksir ( estimator ) titik estimasi interval ( interval estimation ) menguji ketepatan sampling. Secara umum pengertian distribusi binomial dapat ditulis seperti di atas. Pengujian dua proporsi digunakan ketika akan membandingkan apakah proporsi pada populasi pertama lebih kecil, sama atau lebih besar dibandingkan proporsi pada populasi kedua.
Source: barucontohsoal.blogspot.com
Distribusi sampling proporsi dapat digunakan untuk mengetahui persentase atau perbandingan antara dua hal yang berkomplemen (peristiwa binomial), seperti persentase perokok dan bukan perokok, persentase pemilih dan bukan pemilih di suatu pemilu, dan perbandingan antara pemakai dan bukan pemakai hasil produksi tertentu. Populasi bank, populasi perusahaan reksa dana, dsb. Populasi terbatas unsurnya terbatas berukuran n contoh: Distribusi sampling proporsi dapat digunakan untuk mengetahui persentase atau perbandingan antara dua hal yang berkomplemen (peristiwa binomial), seperti persentase perokok dan bukan perokok, persentase pemilih dan bukan pemilih di suatu pemilu, dan perbandingan antara pemakai dan bukan pemakai hasil produksi tertentu. Untuk ini diperlukan sebuah teori yang dikenal dengan nama distribusi sampling.
Source: soalkumplit.blogspot.com
Dari populasi ini diambil sampel acak berukuran n dan dimisalkan didalamnya ada peristiwa a sebanyak x. Untuk ini diperlukan sebuah teori yang dikenal dengan nama distribusi sampling. Misalkan, kita ingin menaksir m/n,. Untuk pengambilan sampel tanpa pengembalian rumus: Distribusi sampling proporsi dapat digunakan untuk mengetahui persentase atau perbandingan antara dua hal yang berkomplemen (peristiwa binomial), seperti persentase perokok dan bukan perokok, persentase pemilih dan bukan pemilih di suatu pemilu, dan perbandingan antara pemakai dan bukan pemakai hasil produksi tertentu.
This site is an open community for users to share their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site value, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title distribusi proporsi by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
