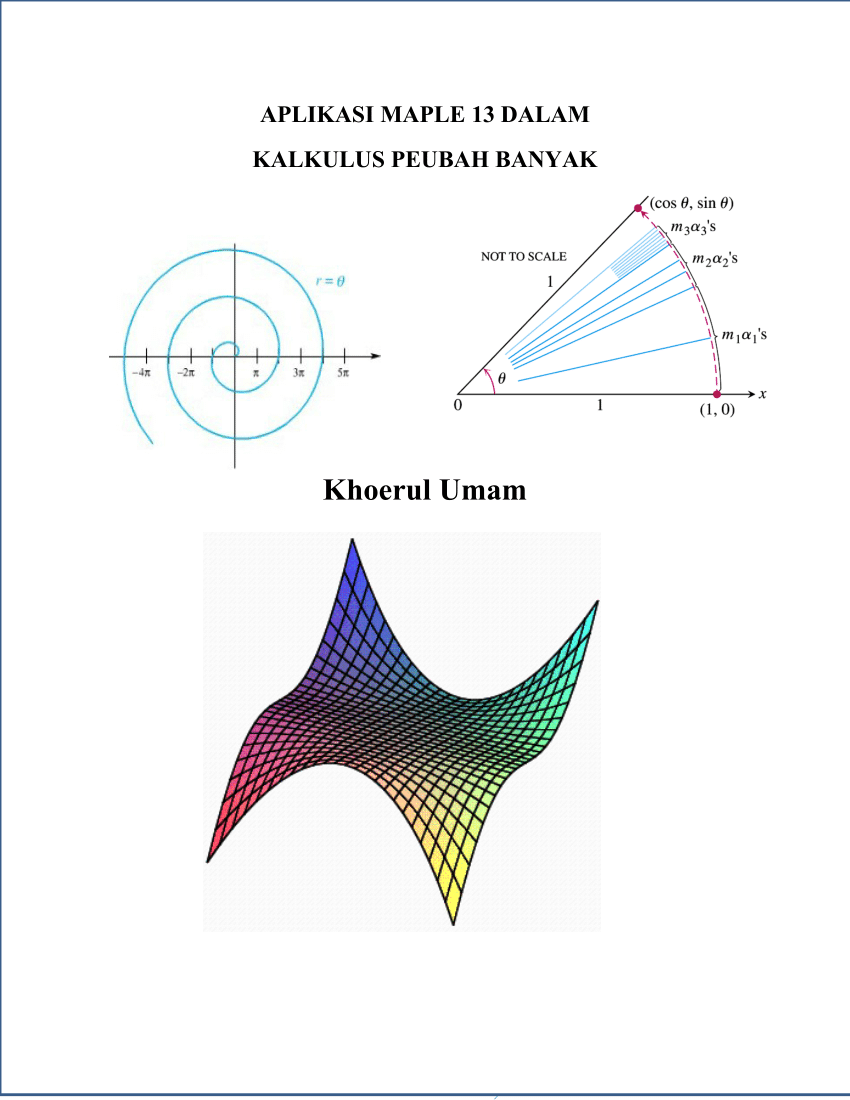
Aturan Sinus Adalah. Aturan sinus dan cosinus 1. Rumus ini disebut sebagai aturan sinus. Luas segitiga = ½ 3.5. Banyak siswa yang kebingungan ketika berhadapan dengan soal tentang aturan sinus dan aturan cosinus.
Konsep 31+ Aturan Sinus From gif.gepics.com
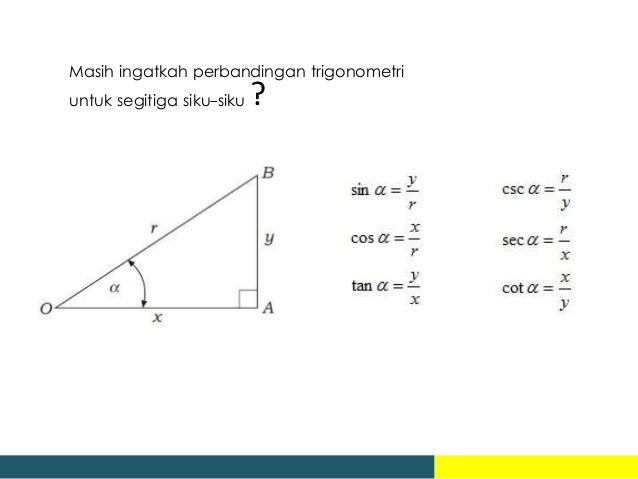
Aturan sinus adalah aturan penting yang berfungsi menghubungkan sisi dan sudut segitiga. Aturan sinus adalah perbandingan antara panjang sisi segitiga dengan sinus menghadap nya yang memiliki nilai sama. Pada segitiga sembarang, sisi miring segitiga tidak dapat ditentukan. Untuk lebih jelasnya, perhatikan gambar dibawah ini : 12 s i n 60 ∘ = a b s i n 45 ∘. Untuk mempermudah anda mengerjakan soal, perhatikan rumus perkalian cosinus dan sinus berikut ini.
Ayo sobat hitung, buat melatih pemahaman kita tentang aturan trigonometri (aturan sinus, aturan cosinus, dan aturan luas) segitiga boleh dicoba latihan soal berikut:
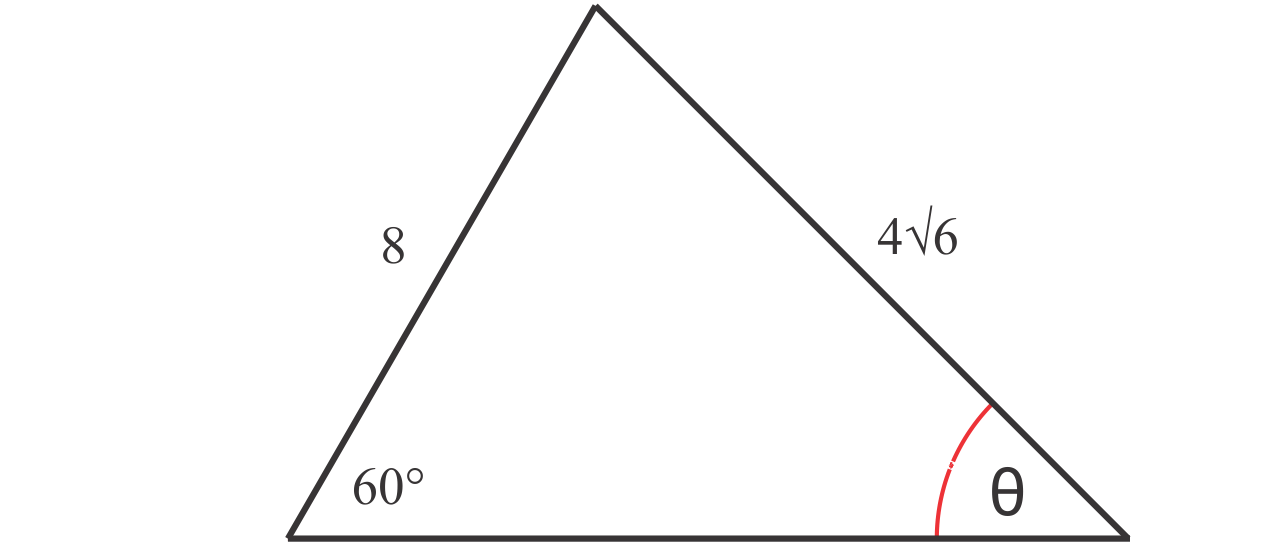
12 s i n 60 ∘ = a b s i n 45 ∘. A b = 12 ⋅ 1 2 2 1 2 3 = 12 2 3 ⋅ 3 3 = 12 6 3 = 4 6 cm. (sin a) / a = (sin b) / b. Ayo sobat hitung, buat melatih pemahaman kita tentang aturan trigonometri (aturan sinus, aturan cosinus, dan aturan luas) segitiga boleh dicoba latihan soal berikut: Aplikasi trigonometri yang sering kita gunakan adalah dikenal dengan aturan sinus, aturan cosinus dan luas segitiga. Materi dan contoh soal + pembahasan.
Source: contoh-surat.co
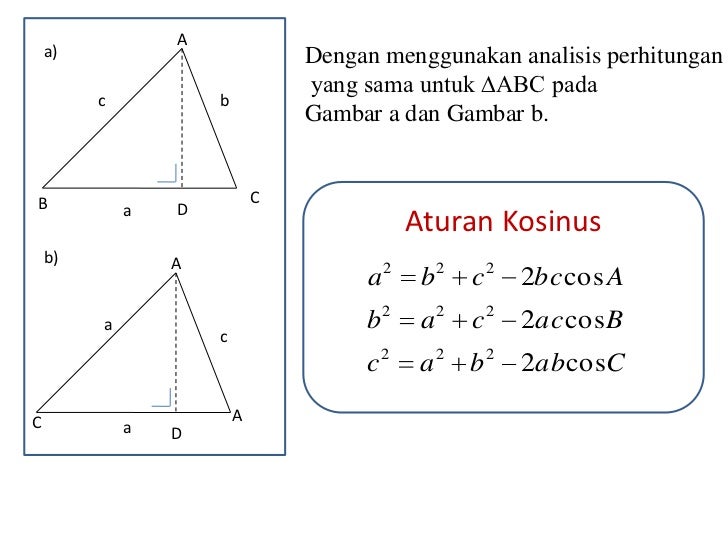
Sin 30 o = ½.3.5.½ = 15/4 = 3,75 cm. Pengertian aturan sinus ialah persamaan yang memaparkan hubungan antara tiga sisi dan tiga sudut pada segitiga sembarang. Jika diberikan segitiga sembarang $abc$ seperti gambar, maka berlaku persamaan berikut. Aturan sinus berlaku untuk segitiga sembarang dan digunakan untuk menyelesaikan soal yang melibatkan dua sudut (diketahui atau pun ditanyakan). Untuk mempermudah anda mengerjakan soal, perhatikan rumus perkalian cosinus dan sinus berikut ini.
Source: lembaredu.github.io
(sin a) / a = (sin b) / b. (sin a) / a = (sin b) / b. Karena itu, petanyaan yang harus dijawab adalah berapakah panjang ab? Untuk mempermudah anda mengerjakan soal, perhatikan rumus perkalian cosinus dan sinus berikut ini. Keterangan a = besar sudut dihadapan sisi a
Source: defantri.com
Pada segitiga pqr di bawah ini, rumus untuk mencari pq adalah. Garis tinggi adalah suatu garis yang dibentuk dari suatu sudut dan berpotongan tegak lurus dengan sisi di hadapannya. Secara umum pembahasan ini disediakan selama sekolah menengah dan termasuk dalam bab trigonometri. Aturan sinus adalah perbandingan panjang sisi sebuah segitiga dengan sinus sudut yang menghadapnya memiliki nilai yang sama. Garis cp merupakan garis tinggi segitiga abc, dimana cp ┴ cb.
Source: idschool.net
12 s i n 60 ∘ = a b s i n 45 ∘. Aturan sinus adalah perbandingan antara panjang sisi segitiga dengan sinus menghadap nya yang memiliki nilai sama. (sin a) / a = (sin b) / b. Ayo sobat hitung buat melatih pemahaman kita tentang aturan trigonometri aturan sinus aturan cosinus dan aturan luas segitiga boleh dicoba latihan soal berikut. Dalam beberapa soal trigonometri melibatkan berbagai hal terkait segitiga dan kita kadang bingung aturan.
Source: lembaredu.github.io
Untuk lebih jelasnya, perhatikan gambar dibawah ini : Aturan sinus adalah aturan penting yang berfungsi untuk menghubungkan sisi dan sudut segitiga. Materi kita hari ini adalah tentang aturan sinus dan kosinus. B c s i n a = a b s i n c. Garis tinggi adalah suatu garis yang dibentuk dari suatu sudut dan berpotongan tegak lurus dengan sisi di hadapannya.
Source: brainly.co.id
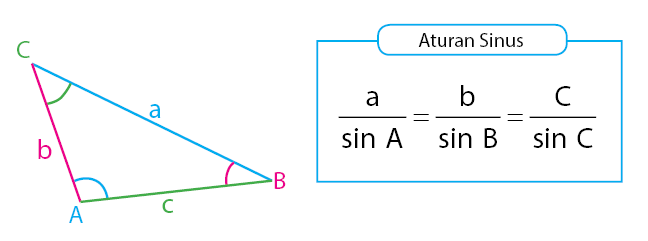
Aturan sinus (law of sines atau sines law/rule) adalah teorema berupa persamaan yang menghubungkan nilai sinus sudut dalam segitiga dengan panjang sisi di depannya dalam bentuk perbandingan. Aturan sinus ini digunakan pada segitiga sembarang untuk menentukan panjang sisinya. Aturan sinus adalah perbandingan antara panjang sisi segitiga dengan sinus menghadap nya yang memiliki nilai sama. Jika diberikan segitiga sembarang $abc$ seperti gambar, maka berlaku persamaan berikut. Untuk lebih jelasnya, perhatikan gambar dibawah ini :
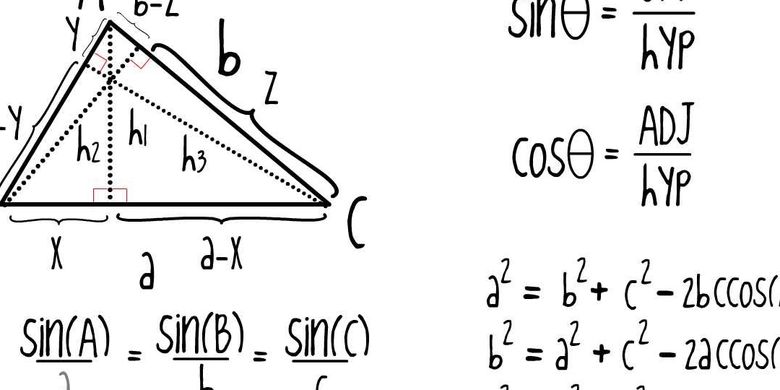Source: rahulgonzales.blogspot.com
Materi kita hari ini adalah tentang aturan sinus dan kosinus. 12 1 2 3 = a b 1 2 2. A b = 12 ⋅ 1 2 2 1 2 3 = 12 2 3 ⋅ 3 3 = 12 6 3 = 4 6 cm. Garis cp merupakan garis tinggi segitiga abc, dimana cp ┴ cb. Aturan sinus adalah aturan penting yang berfungsi menghubungkan sisi dan sudut segitiga.
Source: lembaredu.github.io
Jadi panjang a b = 4 6 cm. Garis cp merupakan garis tinggi segitiga abc, dimana cp ┴ cb. Garis tinggi adalah suatu garis yang dibentuk dari suatu sudut dan berpotongan tegak lurus dengan sisi di hadapannya. Untuk lebih jelasnya, perhatikan gambar dibawah ini : Secara umum, pembahasan ini disediakan selama sekolah menengah dan termasuk dalam bab trigonometri.
Source: ruangilmu.github.io
Selain itu aturan sinus juga berguna untuk menentukan sudut pada segitiga yang besarnya belum diketahui. Garis tinggi adalah suatu garis yang dibentuk dari suatu sudut dan berpotongan tegak lurus dengan sisi di hadapannya. Aturan sinus (law of sines atau sines law/rule) adalah teorema berupa persamaan yang menghubungkan nilai sinus sudut dalam segitiga dengan panjang sisi di depannya dalam bentuk perbandingan. Aturan sinus adalah aturan penting yang berfungsi menghubungkan sisi dan sudut segitiga. Ayo sobat hitung buat melatih pemahaman kita tentang aturan trigonometri aturan sinus aturan cosinus dan aturan luas segitiga boleh dicoba latihan soal berikut.
Source: gif.gepics.com
Aturan sinus menyatakan bahwa perbandingan panjang sisi sebuah segitiga dengan sinus sudut yang menghadapnya memiliki nilai yang sama. 12 s i n 60 ∘ = a b s i n 45 ∘. Untuk mempermudah anda mengerjakan soal, perhatikan rumus perkalian cosinus dan sinus berikut ini. Contoh soal ini merupakan lanjutan dari pembahasan aturan sinus yang telah dibahas sebelumnya sehingga model soal yang akan diberikan adalah menentukan rumus aturan sinus pada segitiga sebarang, menentukan. Rumus aturan sinus dan cosinus.
Source: haloedukasi.com
Jadi panjang a b = 4 6 cm. Pada segitiga sembarang, sisi miring segitiga tidak dapat ditentukan. 12 s i n 60 ∘ = a b s i n 45 ∘. Untuk mempermudah anda mengerjakan soal, perhatikan rumus perkalian cosinus dan sinus berikut ini. 12 1 2 3 = a b 1 2 2.
Source: mataseluruhdunia208.blogspot.com
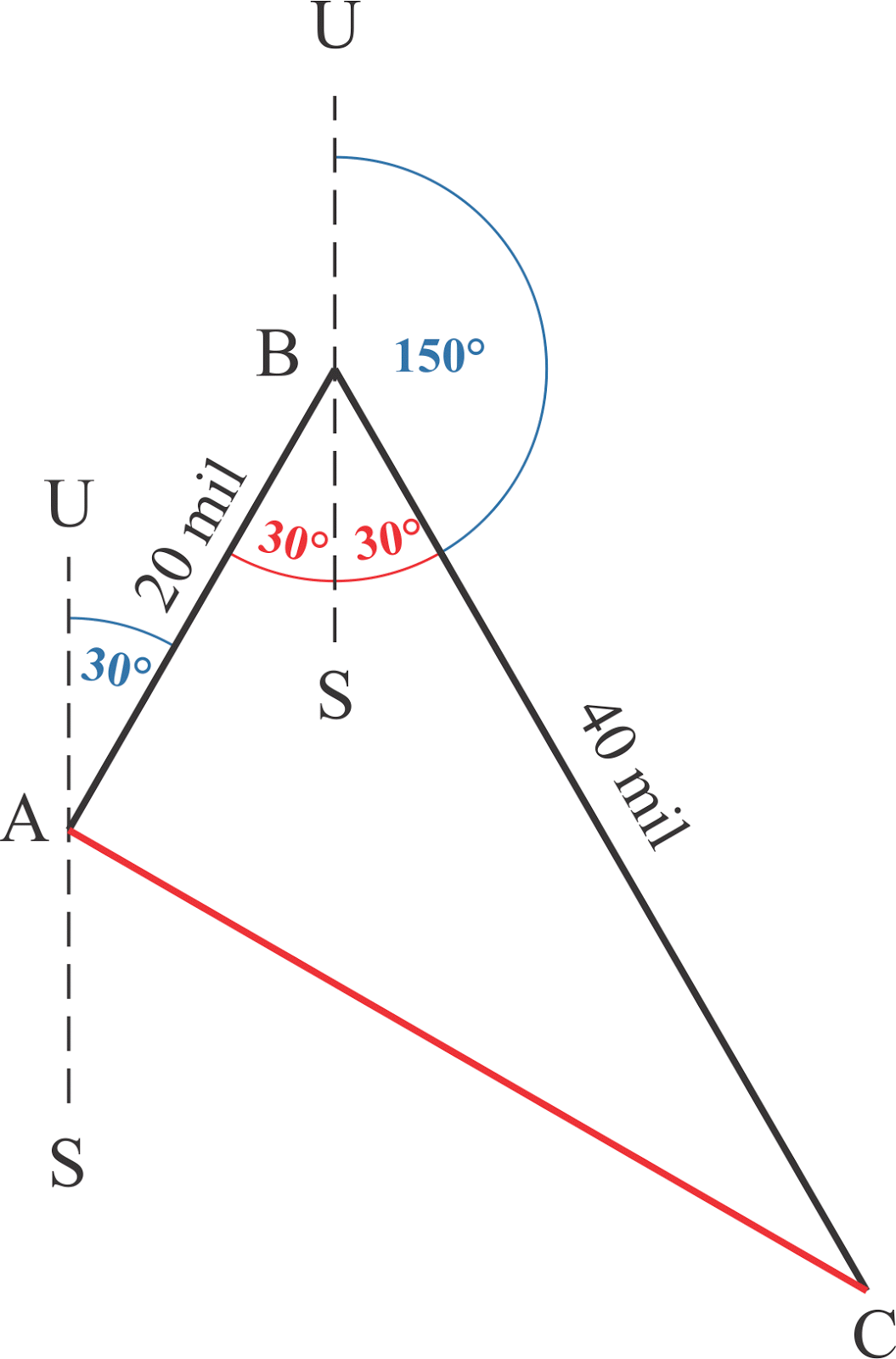
Aturan cosinus merupakan aturan yang menjelaskan hubungan antara kuadrat panjang sisi dengan nilai cosinus dari salah satu sudut pada segitiga. 12 1 2 3 = a b 1 2 2. 15 agar kita dapat menentukan jarak ab maka kita memerlukan gambar seperti disamping. Aturan sinus adalah perbandingan antara panjang sisi segitiga dengan sinus menghadap nya yang memiliki nilai sama. Aturan sinus (law of sines atau sines law/rule) adalah teorema berupa persamaan yang menghubungkan nilai sinus sudut dalam segitiga dengan panjang sisi di depannya dalam bentuk perbandingan.
Source: rumuspintar.com
12 1 2 3 = a b 1 2 2. Jika diberikan segitiga sembarang $abc$ seperti gambar, maka berlaku persamaan berikut. Aturan sinus adalah perbandingan antara panjang sisi segitiga dengan sinus menghadap nya yang memiliki nilai sama. Ayo sobat hitung buat melatih pemahaman kita tentang aturan trigonometri aturan sinus aturan cosinus dan aturan luas segitiga boleh dicoba latihan soal berikut. Aturan sinus memperlihatkan perbandingan panjang sisi dengan sinus sudut.
Source: contoh-surat.co
(sin a) / a = (sin b) / b. Sebagai pelengkap pembuktian, berikut disampaikan juga bagaimana penurunan rumus aturan sinus yang diperoleh dari segitiga tumpul. Aturan sinus berlaku untuk segitiga sembarang dan digunakan untuk menyelesaikan soal yang melibatkan dua sudut (diketahui atau pun ditanyakan). Aturan sinus berbunyi bahwa perbandingan panjang sisi sebuah segitiga dengan sinus sudut yang menghadapnya memiliki nilai yang sama. 12 s i n 60 ∘ = a b s i n 45 ∘.
Source: amranhapsan.com
Misalnya pada segitiga abc yang memiliki panjang sisi a, b, dan c, serta sudut a, b, c, maka aturan sinus yang berlaku adalah sebagai berikut. Luas segitiga = ½ 3.5. Jadi panjang a b = 4 6 cm. Aturan sinus memperlihatkan perbandingan panjang sisi dengan sinus sudut. 12 1 2 3 = a b 1 2 2.
Source: rakhi.mobi
Pada segitiga pqr di bawah ini, rumus untuk mencari pq adalah. Aturan sinus adalah aturan penting yang berfungsi untuk menghubungkan sisi dan sudut segitiga. Rumus aturan sinus dan cosinus. Secara umum pembahasan ini disediakan selama sekolah menengah dan termasuk dalam bab trigonometri. Garis tinggi adalah suatu garis yang dibentuk dari suatu sudut dan berpotongan tegak lurus dengan sisi di hadapannya.
Source: gif.gepics.com
Untuk lebih jelasnya, perhatikan gambar dibawah ini : Materi kita hari ini adalah tentang aturan sinus dan kosinus. 4 menggunakan aturan sinus untuk menentukan panjang sisi atau besar sudut pada segitiga. Aplikasi trigonometri yang sering kita gunakan adalah dikenal dengan aturan sinus, aturan cosinus dan luas segitiga. Garis tinggi adalah suatu garis yang dibentuk dari suatu sudut dan berpotongan tegak lurus dengan sisi di hadapannya.
Source: smatika.blogspot.com
Pada segitiga pqr di bawah ini, rumus untuk mencari pq adalah. Aturan sinus adalah aturan penting yang berfungsi untuk menghubungkan sisi dan sudut segitiga. 12 s i n 60 ∘ = a b s i n 45 ∘. A b c = = sina sinb sinc rumus terakhir dikenal dengan aturan sinus contoh soal • pada segitiga abc diketahui ∠ a = 30o, ∠ b = 45o dan sisi a = 6 cm. Aturan sinus dan cosinus 1.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title aturan sinus adalah by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
